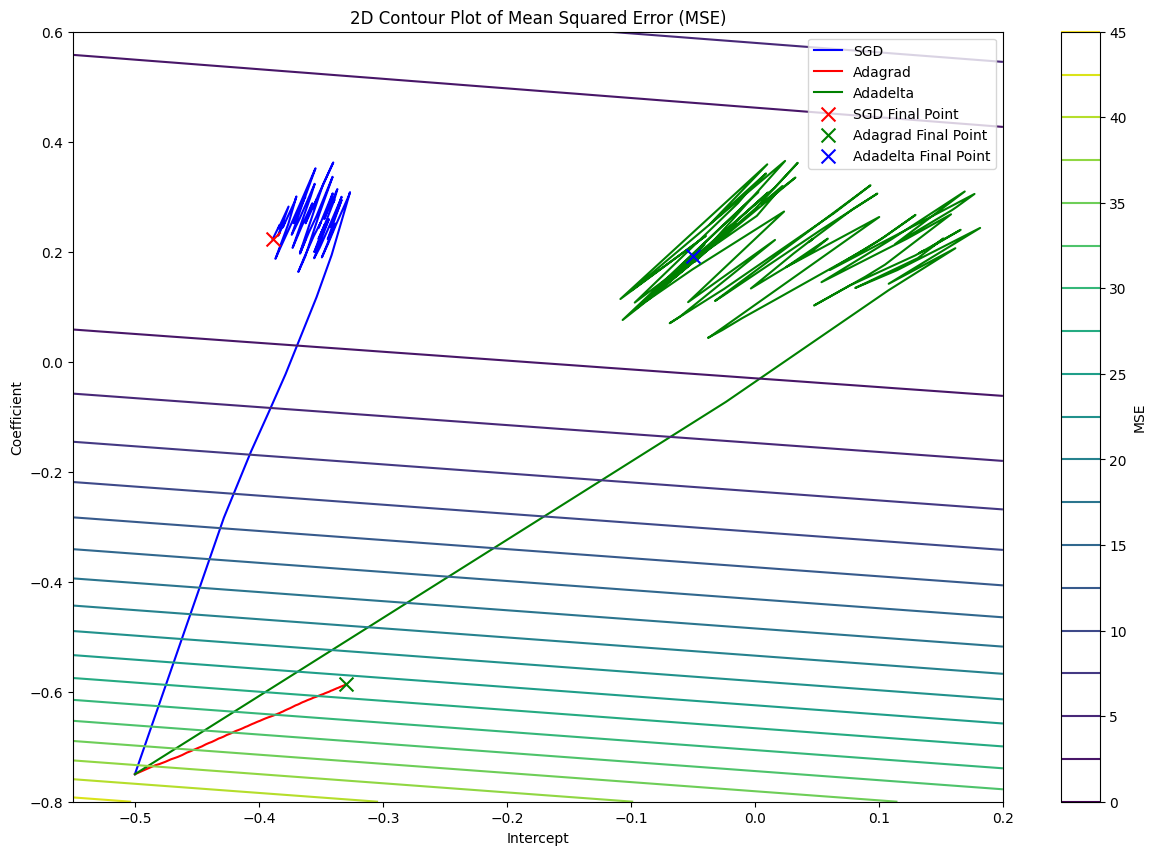
Reducing the aggresive learning rate decay in Adagrad
Remember that in Adagrad, we have see that each parameter has its own learning rate. However, the learning rate is rapidly decreasing as the number of iterations increases. This can be a problem because the learning rate can become too small and the model stops learning.
In this post, we will see how Adadelta prevents learning rate decreasing rapidly over time. Instead of inefficiently storing, or summing, all the past squared gradients, Adadelta calculates the average of the decayed past gradients and uses it to update parameters. Most importantly, Adadelta uses no learning rate.
The parameter update rule is expressed as
where
, the root mean square of parameters up to time , can be expressed as follows:
where is the mean squared parameter updates up to time .
, the root mean square of gradients up to time , can be expressed as follows:
where is the mean squared gradients up to time .
and are the gradients of the cost function with respect to the intercept and the coefficient respectively, and can be expressed as follows:
First, define a function that calculates the root mean square of the values.
def rms(past_values, current_value, momentum=0.9, eps=1e-8): average = momentum * np.mean(past_values**2) + (1 - momentum) * current_value**2 return np.sqrt(average + eps)Second, calculate the intercept and the coefficient gradients. Notice that the intercept gradient is the prediction error.
new_intercept_gradient = errornew_coefficient_gradient = error * x[random_index] Third, we need to determine . Since we have define the function rms() in the beginning,
we can calculate the root mean square of the gradients.
coefficient_gradient_rms = rms(df['coefficient_gradient'].values, new_coefficient_gradient)intercept_gradient_rms = rms(df['intercept_gradient'].values, new_intercept_gradient) Fourth, we need to determine , and we are going to do the same
but we are going to apply the function on the intercept and the coefficients columns.
intercept_rms = rms(df['intercept'].values[:epoch], intercept)coefficient_rms = rms(df['coefficient'].values[:epoch], coefficient)Finally, we can update the intercept and the coefficient.
delta_intercept = -(intercept_rms / intercept_gradient_rms) * new_intercept_gradientdelta_coefficient = -(coefficient_rms / coefficient_gradient_rms) * new_coefficient_gradient
intercept += delta_interceptcoefficient += delta_coefficient 
With Adadelta, we can reach the minimum point of the cost function faster than Vanilla SGD and Adagrad. Thus, it allows us to explore more in the parameter space and find the optimal parameters for the model.
def adadelta(x, y, df, epochs=100): intercept, coefficient = -0.5, -0.75 random_index = np.random.randint(len(features)) prediction = predict(intercept, coefficient, x[random_index]) error = prediction - y[random_index] df.loc[0] = [intercept, coefficient, error, error * x[random_index], (error ** 2) / 2]
for epoch in range(1, epochs + 1): random_index = np.random.randint(len(features)) prediction = predict(intercept, coefficient, x[random_index]) error = prediction - y[random_index]
new_intercept_gradient = error new_coefficient_gradient = error * x[random_index]
intercept_rms = rms(df['intercept'].values[:epoch], intercept) coefficient_rms = rms(df['coefficient'].values[:epoch], coefficient)
intercept_gradient_rms = rms(df['intercept_gradient'].values, new_intercept_gradient) coefficient_gradient_rms = rms(df['coefficient_gradient'].values, new_coefficient_gradient)
delta_intercept = -(intercept_rms / intercept_gradient_rms) * new_intercept_gradient delta_coefficient = -(coefficient_rms / coefficient_gradient_rms) * new_coefficient_gradient
intercept += delta_intercept coefficient += delta_coefficient
mse = (error ** 2) / 2
df.loc[epoch] = [intercept, coefficient, new_intercept_gradient, new_coefficient_gradient, mse]
return df